Integrals with a singularity
When there is a singularity in the function being integrated such that the integral becomes undefined, it is not , then C does not need to be the same on both sides of the singularity. The forms below normally assume the a singularity in the value of C but this is not in general necessary. For instance in
There is a singularity at 0 and the integral becomes infinite there. If the integral above was used to give a definite integral between -1 and 1 the answer would be 0. This however is only the value assuming the Cauchy principal value for the integral around the singularity. If the integration was done in the complex plane the result would depend on the path round the origin, in this case the singularity contributes −iπ when using a path above the origin and iπ for a path below the origin. A function on the real line could use a completely different value of C on either side of the origin as Rational functions
These rational functions have a non-integrable singularity at 0 for a ≤ −1.
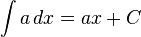 Exponential functions
Exponential functions
- more integrals:exponitial funmtion
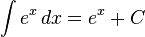

Logarithms
- more integrals:logrthmic funtion


Trigonometric functions
- more integrals:trigonomertic funtion



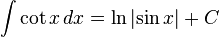








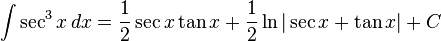
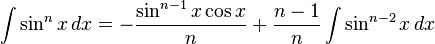

Inverse trigonometric functions
Hyperbolic functions
Inverse hyperbolic functions
Composed functions
Absolute value functions
Special functions
Ci, Si: Trignometry integrals, Ei: Exponential integrals, li: Logarithmic integral function, erf: Error function
Definite integrals lacking closed-form antiderivatives
There are some functions whose antiderivatives cannot be expressed in closed form . However, the values of the definite integrals of some of these functions over some common intervals can be calculated. A few useful integrals are given below.
 when a > 0
when a > 0
 when a > 0, n is 1,2,3,... and !! is the double factional
when a > 0, n is 1,2,3,... and !! is the double factional
 when a > 0
when a > 0
 when a > 0, n is 0, 1, 2, ....
when a > 0, n is 0, 1, 2, ....
 (
(
 (
(
 (if n is an even integer and
(if n is an even integer and  )
)
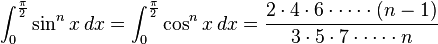 (if
(if  is an odd integer and
is an odd integer and 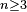 )
)
 (for
(for  integers with
integers with  and
and 
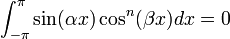 (for
(for  real and
real and  non-negative integer,
non-negative integer,
 (for
(for  integers with
integers with  and
and 
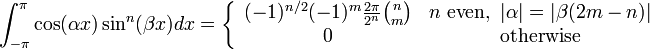 (for
(for  integers with
integers with  and
and 
 (where Γ(z) is the gamma funtion
(where Γ(z) is the gamma funtion
![\int_{-\infty}^\infty e^{-(ax^2+bx+c)}\,dx=\sqrt{\frac{\pi}{a}}\exp\left[\frac{b^2-4ac}{4a}\right]](http://upload.wikimedia.org/math/3/1/8/31880cca3462a0bd5cc1e00bbc790da9.png) ( eu, and a > 0)
( eu, and a > 0)
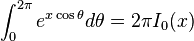 (
(
 ,
, 0\," src="http://upload.wikimedia.org/math/8/7/e/87ecc6d98450874d2b57cbc8e56ffdd1.png">,






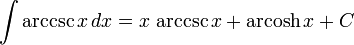









![\int \operatorname{arcsch}\,x \, dx = x\, \operatorname{arcsch}\, x+ \ln{\left[x\left(\sqrt{1+\frac{1}{x^2}} + 1\right)\right]} + C](http://upload.wikimedia.org/math/7/7/b/77b4c1f2e3e5c68d58f0bff1817543aa.png)


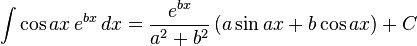



![\int \left| (ax + b)^n \right|\,dx = {(ax + b)^{n+2} \over a(n+1) \left| ax + b \right|} + C \,\, [\,n\text{ is odd, and } n \neq -1\,]](http://upload.wikimedia.org/math/a/e/d/aed4376248ecab33b3d87d34bee387a8.png)


![\int \left| \tan{ax} \right|\,dx = {\tan(ax)[-\ln\left|\cos{ax}\right|] \over a \left| \tan{ax} \right|} + C](http://upload.wikimedia.org/math/3/d/2/3d209aa00c94b48b778a62b117fe4536.png)
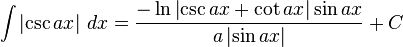

![\int \left| \cot{ax} \right|\,dx = {\tan(ax)[\ln\left|\sin{ax}\right|] \over a \left| \tan{ax} \right|} + C](http://upload.wikimedia.org/math/2/5/8/2588f0de19ae2908567c52eb20c8bbfa.png)



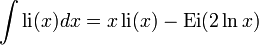









![\int_0^1 [\ln(1/x)]^p\,dx = p!](http://upload.wikimedia.org/math/e/c/1/ec1121d71b043a358803b3439e6b6a45.png)

No comments:
Post a Comment